Solving combinatorial optimization problems related to production planning
FLEXSCHE Optimizer
FLEXSCHE Optimizer
The "FLEXSCHE Optimizer" solves combinatorial optimization problems related to production planning.
Production scheduling problems are generally combinatorial optimization problems, and many methods have been researched to solve them. However, when trying to find an exact optimal solution with a generic model, the combinations become enormous, making it difficult to solve. Therefore, FLEXSCHE, as a general-purpose production scheduler, has adopted a rule-based approach to find a "better" feasible solution within a realistic time frame, rather than using mathematical optimization methods that cannot reach a solution in a realistic time.
However, finely adjusting scheduling rules requires advanced technical skills. Especially when factors such as changeovers or batch furnace lot combinations, which greatly affect production efficiency and on-time delivery rates, come into play, simply arranging operations in "due date order" will not yield satisfactory planning results. To achieve sufficient results, meticulous adjustment of scheduling rules is necessary. Constructing such scheduling rules is akin to algorithm development, requiring high proficiency costs, and training engineers capable of handling it is also challenging.
To overcome such difficult situations, the "FLEXSCHE Optimizer" was released.
The "FLEXSCHE Optimizer" solves combinatorial optimization problems related to production scheduling using mathematical optimization methods. By combining it with the rule-based scheduling of FLEXSCHE, it is possible to limit the search space and find the optimal solution while reaching a solution within a realistic time frame.
Minimize Overdue
Dynamic Changeover × Strict Deadlines
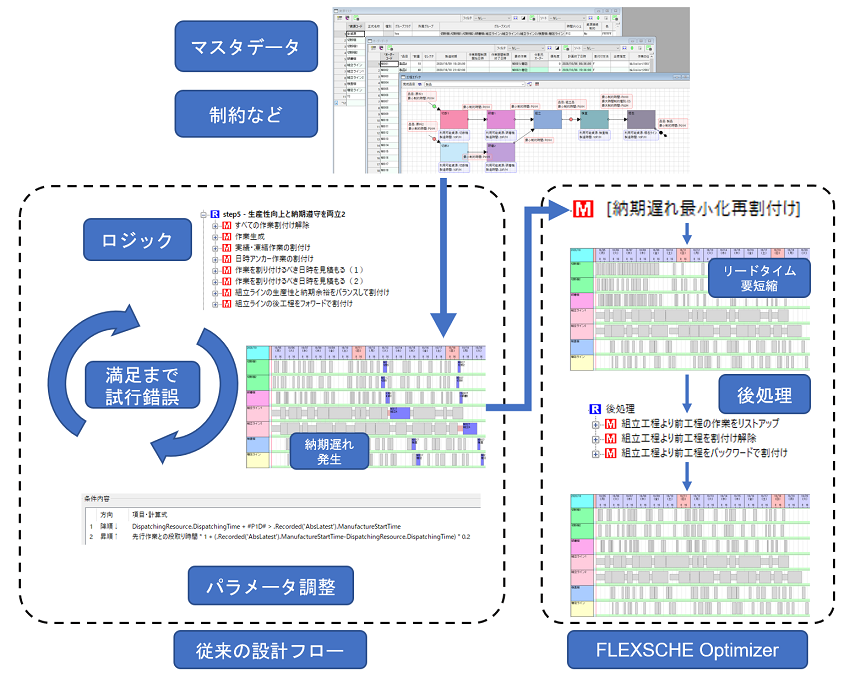
Consider a case where there is a dynamic changeover constraint, where the preparation time changes depending on the order of operations, and strict deadlines are imposed. If you respond with existing functions, a method using the "Resource-driven Dispatching" method can be considered to control the order of operations on resources by considering both changeover time and deadlines. However, to achieve this, it is also necessary to extract bottlenecks, identify the target processes for order control, and analyze the distribution of operation time and dynamic changeover time while complying with inter-process constraints, tuning multiple parameters simultaneously. All of these require a lot of trial and error, leading to increased costs and risks of implementation. (See "Conventional Design Flow" in the diagram below)
In contrast, the "Minimize Overdue Reassignment" method targets assigned operations and automatically searches for a configuration with less overdue from all configurations that meet the constraints (including upstream and downstream) using mathematical optimization methods, starting from the assigned state before the method execution. Even starting from the default rule planning result, which simply arranges in due date order, a plan with no overdue or improved on-time delivery rate can be obtained. Furthermore, if a better initial plan is provided, it is expected to obtain an optimal planning result in a shorter time.
Cutting Plan
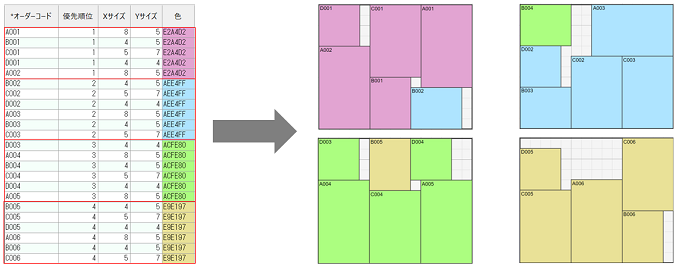
Consider cutting out a group of rectangular products of specific sizes from a rectangular raw material. In this case, you want to cut out as little scrap as possible. Additionally, various conditions are actually required, such as prioritizing products based on order deadlines or cutting out products A and B simultaneously.
If it were only the cutting problem, there might have been tools to solve it in the past. However, in production planning, it is necessary to solve this problem in combination with production scheduling. By solving the cutting problem with the "FLEXSCHE Optimizer" while combining it with traditional scheduling methods, a high-quality "Cutting Plan" can be realized.
Loop Painting Line Circulation Plan
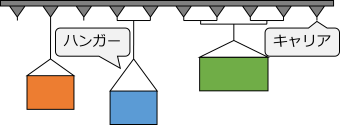
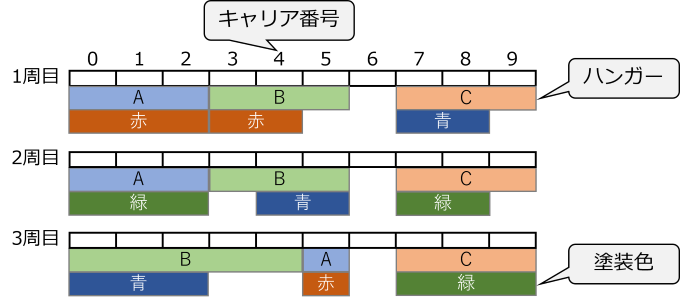
On a circulating conveyor, carriers are attached, and hangers are hung on them. Products are hung on these hangers, and they are painted when passing through the painting booth located along the conveyor. The paint color and available hangers are determined for each order.
Hangers are heavy, so they should be reused as much as possible without detaching them. Once a hanger is hung, it can be used in subsequent circulations without removal. For example, on carrier 0, the hanger changes in the second and third circulations, but on carrier 4, the same hanger is used throughout.
Also, when the paint color changes in the painting booth, a changeover occurs, and products should not be placed on hooks passing through during that time. For example, carrier 6 in the second circulation is empty to switch the paint color from blue to green.
The goal is to minimize the number of hanger detachments while considering changeovers so that all daily operations fit into the plan. In this example, there are a total of 4 locations where the carrier changes hangers, so the number of hanger detachments is calculated as 4 times.
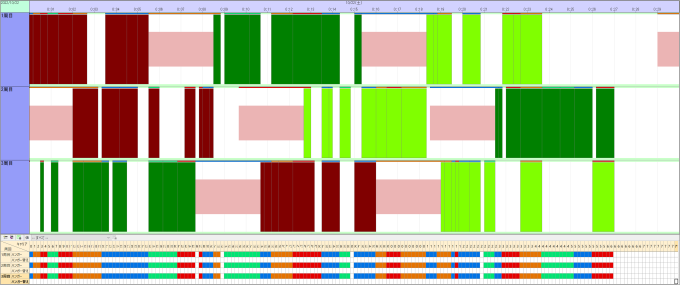
The result of planning using this function is shown in the image. In the Gantt chart above, the color of the operation represents the paint color, and the color of the bar on the operation represents the type of hanger. A pink changeover is inserted between operations of different paint colors. The plan, focusing on hangers, is made easier to see in the data cube viewer below, confirming that the hangers on each carrier are aligned in the same color across circulations, resulting in a plan that does not require hanger detachment.
To plan such a schedule, it is necessary to consider changeovers within the same circulation and hanger detachments between circulations, but achieving this with conventional scheduling rules requires constructing complex rules, which is quite challenging. By using the "Loop Painting Line Circulation Plan" function, this part can be entrusted to the Optimizer without complex settings.